What is Ticket to Ride?
The objective of Ticket to Ride is to earn the most points via laying "trains" on pre-determined railroad tracks all over Europe. More specifically, players earn points by:
- Completing “ticket” cards - each player aims to fulfill at least three “tickets,” which direct you from starting points on the board to different endpoints. There are 46 ticket cards in Ticket to Ride: Europe.
- Building “routes” - each pathway between adjacent cities is called a “route.” Routes are of predetermined length on the board. The longer the route, the more points you earn.
- Building the longest unbroken train route - players can earn 10 extra points at the end of the game for building the longest unbroken route. This is important because players are not only incentivized to get from point A to point B as efficiently as possible. Taking a more circuitous route could end up earning you more points, but at the risk of failing to fulfill you “ticket” cards.
- A few other ways that are not as relevant to the analysis below.
Why analyze the game?
The original Github Repo (by Rob Bettles) that inspired this project analyzes the United States version of the board. The central goal of Bettles' analysis is the same as the one found in this repo: to determine whether or not particular train routes have a higher probability of being occupied by the end of the game. If certain routes are more likely to be occupied, players might use this information to inform their game strategy.
The "Europe" version of the game has a few new rules added to the mix, and I’m interested in seeing if they have any impact on the probability of certain routes being taken over the course of the game.
To the left, you can see every city on the Ticket to Ride: Europe Board. Paris is a crucial node in the train network, with 10 total routes going in and out of the city. This also means that Paris is likely to be more crowded than other cities on the map, making it desirable to players aiming to either claim it early or block it from others. Meanwhile, the cities on the edges of the board, while offering fewer routes, are less likely to be taken by the end of the game. Players aiming to create circuitous routes around the board, or who hope to avoid traffic, might opt for these routes.
Analysis
Following Bettles' code almost exactly, I applied Dijkstra's algorithm to the Ticket to Ride board in Python script. In doing so, I was able to determine the shortest route from one node (city) on the board to another. Analysis via NetworkX also allowed me to track the exact route a player would take to move in the most efficient way from each ticket card's origin city to its destination city.
In each of the visualizations below, the darker the route between cities, the more ticket cards it contributes to when players are fulfilleing their respective ticket cards' origin and destination cities.
But each visualization differs slightly.
For every ticket card, there are multiple ways to move from Point A, the origin city, to Point B. Each visualization below uses a different number of possibilities a player might take to fulfill their ticket.
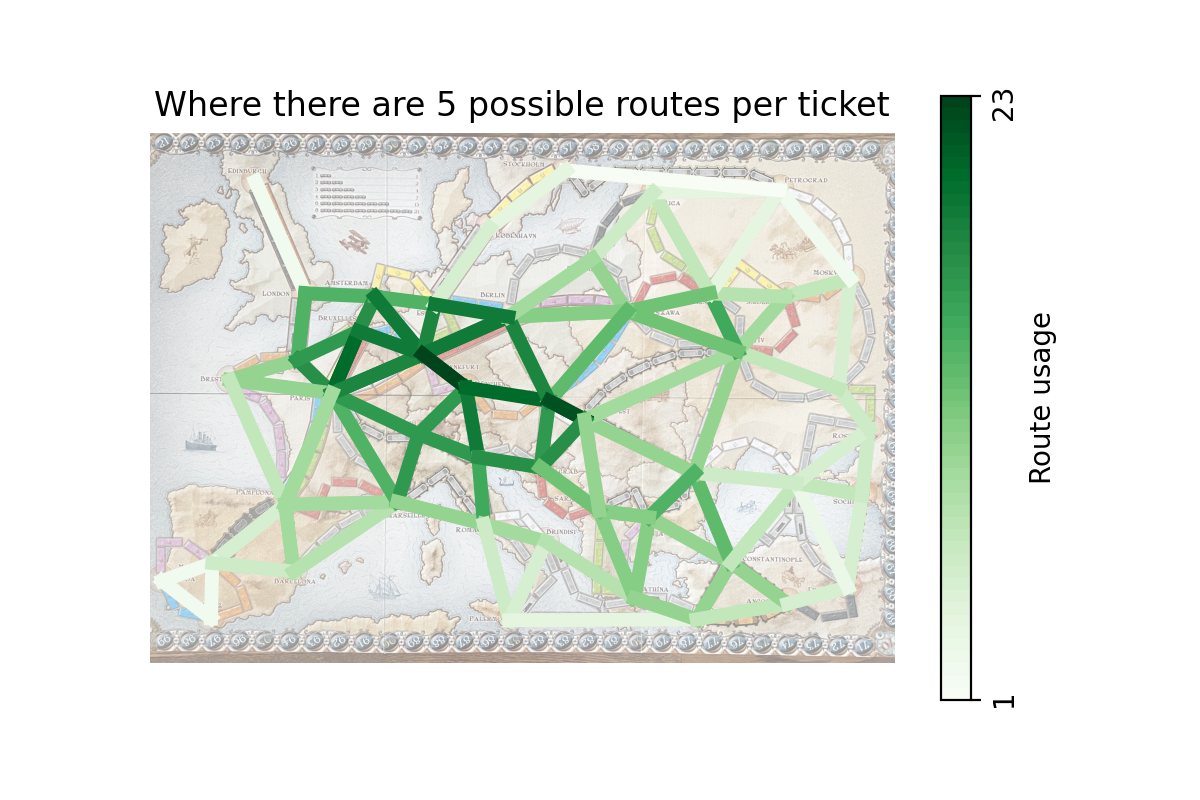
In the above scenario, every ticket card has five possible "paths" to get from its origin to its destination. The darker the route, the more likely it is to be taken by a player. We can see that the center of the board has a heavy concentration of darker routes. Not only are these routes more likely to serve as connections on-route to a player's destination, but these routes also tend to be shorter, making them easier to claim.

But there are more than just five possible paths per ticket. Here, we are examining the likelihood of routes to be taken out of the 10 shortest possible paths to complete each ticket.
This number is bumped to 10 because perhaps five possible paths isn’t enough. Let’s say you’re trying to get from Palermo, Italy to Moscow, Russia — a ticket worth 21 points. You have many options to make that connection, but with those options come obstacles and decisions.
For example, what if your desired routes have been blocked by other players? Or, what if you simply want to take the 10th-shortest route rather than the shortest route, opting to go through particular waypoints that fulfill your other ticket cards? This code looks at the 10-shortest possible paths from Palermo to Moscow and weighs each equally. It repeats this same process for each ticket card.
The result is the map above, which shows us, once again, that routes in the middle of the board are more likely to be used over the course of the game.

Now things are a bit unwieldy. The 20th-shortest route to get from Palermo, Italy to Moscow, Russia might not even exist — and if it does, it’s likely just another way to say “the longest route.”
Regardless, this visualization is still helpful in demonstrating the phenomenon at hand: cities in the middle of the board are more useful than those on the outside when a player is optimizing for the shortest route.
Take Aways
Next time you play Ticket to Ride, keep these keys in mind:
- The board is most likely to be crowded in the middle.
- This means you can go for the middle early, opting to block it from other players or claim it for your own future use.
- Or, you can steer clear of the middle and prioritize circuitous routes. Choosing pathways along the periphery will help you avoid other players and could help you secure extra points for achieving the longest route.